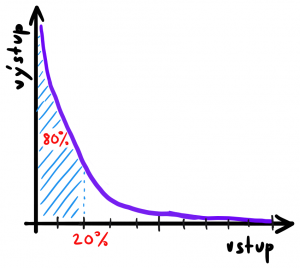
Původně ekonomicky motivovaná Paretova poučka, známá též jako pravidlo 80/20, v zobecněné formě tvrdí, že na vytvoření 80% výstupu obvykle stačí 20% vstupu. Toto jednoduché schéma našlo svou analogii i mimo řadu jiných, neekonomických oblastí. Ačkoliv funguje často docela dobře, je dobré s ním zacházet obezřetně. Paretovo pravidlo není možné nebo rozumné slepě aplikovat na všechny situace. Někdy je dosažení posledních 20% i za cenu vynaložení násobku dosavadních prostředků (resp. času) žádoucí, např. při získávání nějaké dovednosti nebo znalosti, nebo u striktně vymezených projektů, které mají smysl pouze jako celek.
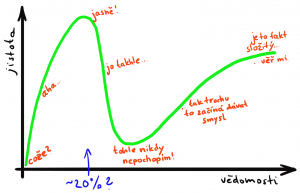
S prvním výše zmíněným příkladem mimochodem souvisí i psychologický jev, kdy pocit „mírně poučených“ v nějakém oboru že tématu rozumí, bývá typicky silnější, než u skutečných expertů daného oboru (tzv. Dunning-Krugerův efekt). S druhým zmíněným příkladem pak souvisí všechny situace, kde se projevuje nějaký synergický efekt, kdy vynechání nějaké části vede k zásadní degradaci výsledku. „Paretova bábovka“ upečená dle klasického receptu s vynecháním jedné ingredience by vám asi moc nechutnala a pochybuji, že byste se ztotožnili s hodnocením, že použitím ingrediencí za 20% celkové ceny (např. mouka + voda) může vzniknout „z 80% perfektní bábovka“.
Stejně jak je zřejmé, že příliš nezáleží na přesných číslech (80/20), spíše jde o empiricky odhalený důsledek toho, že jednotlivé činnosti, ze kterých se nějaký úkol skládá, lze seřadit podle nákladů (ať už finančních, časových, fyzických, duševních, …) a v takovém nerovnoměrném rozdělení pak logicky existuje relativně úzká oblast, jejíž integrál je vyšší, než integrál chvostu tohoto rozdělení. Jednoduše – a obecně bez čísel – řečeno: menší část příčin stojí za větší částí důsledků.
Také bývá častou chybou založit rozhodování o tom, co spadá do horního pásma (ať už to je přesně 20%, nebo více či méně), na špatné nebo neúplné sadě parametrů. Nemůžete se v běžném byznysu například věnovat jen horní pětině zákazníků na základě útraty, kterou jsou u vás ochotni zanechat, protože ve zbylých 80% může být někdo, jehož názor má vliv na rozhodování řady dalších lidí, mezi nimiž můžou být i nějací z vašich prominentních zákazníků. Jinými slovy – do rozhodování vstupují i jiné, než čistě finančně kvantitativní ukazatele.
Problém je, že ne vždy jsou tyto ukazatele známy. Což mě přivedlo k malému zamyšlení, do jaké míry bych mohl aplikovat Paretovo pravidlo na vědeckou činnost. Třeba bych pak přišel na to, jak zefektivnit svou práci (vynechání ranního kafe v tomto směru moc potenciálu neskrývá :).
Budeme-li vycházet z toho, jakým způsobem je v dnešní době typicky věda z vnějšího hlediska posuzována, tak jako jednotku výstupu vědecké práce lze použít publikaci, jako kvantifikátor pak celkem solidně poslouží ohlas ve smyslu počtu citací na daný článek. Za předpokladu zhruba stejného času potřebného na vznik každé jednotky a zanedbání časového faktoru (počet citací samozřejmě monotónně narůstá v čase, takže starší články v průměru stojí výše, ale pokud se průběžně v čase střídají produkce méně a více úspěšných výstupů, pak lze toto zanedbání učinit), pak můžu ze svého současného seznamu publikací vydedukovat, že horních 20% článků vede k zhruba 62% všech citací a na pokrytí 80% „výkonu“ jsem potřeboval 37% článků. Jak už jsem psal výše, na přesných číslech nezáleží, takže bychom v tomto konkrétním případě interpretovali Paretovu poučku jako 62/20 nebo 80/37 a mohli bychom s tím být hotovi. Navíc u jiných autorů to může být jinak a v mnoha případech [1, 2, 3, 4] je na větších vzorcích relace 80/20 poměrně dobře splněna. Jenže hlavní problém je v tom, že pokud má být takové pravidlo použito pro plánování práce, potažmo zvýšení její efektivity, musel bych mít v ruce mechanismus, pomocí kterého předem posoudím, jak si bude který článek nebo (když půjdeme více k podstatě) výzkumné téma stát z hlediska budoucího výsledku. Pokud bych něco takového měl, asi bych tomu dál těžko mohl říkat výzkum.
Zdá se tedy, že Paretovo pravidlo může být velmi užitečné, tím spíše když jeho aplikaci předchází ujasnění si toho, kolik nás která činnost stojí úsilí nebo času a kolik nám ve výsledku přináší. Zároveň se ukazuje jedno z jeho principiálních omezení, tj. že je možné ho uplatňovat spíše na činnosti rutinní povahy, ale nikoliv na tvůrčí činnosti (nikoliv nutně pouze vědecké), kde je možnost predikovat výsledek velmi omezená.
